Introduction
In my last article I wrote about my experiences using the Poisson distribution to predict the outcome of football matches. The results so far have been rather disappointing so I thought I would have a look at where things were going wrong.
Probabilities
The first place I decided to look was at the probabilities generated for the matches predicted correctly compared with those predicted incorrectly. I suspected that maybe the model was struggling with matches between more evenly matched teams. For example, for last week’s match between Stoke and Sunderland the predicted outcome was a home win with a probability of 51%. This still leaves us with a 49% chance though that the game will finish with an away win or a draw instead making it potentially difficult to predict accurately.
Overall, the average probability for games correctly predicted was 64% compared with 56% in the games where the prediction failed. At first look it would therefore appear that the model does struggle somewhat with games between more closely matched teams. However, when you look at the variability in the data it is not possible to discern between the two percentages (Figure 1). In fact comparing the data sets using analysis of variance (ANOVA) gives a p-value of 0.32 suggesting no statistical difference between the two percentages based on the current data.
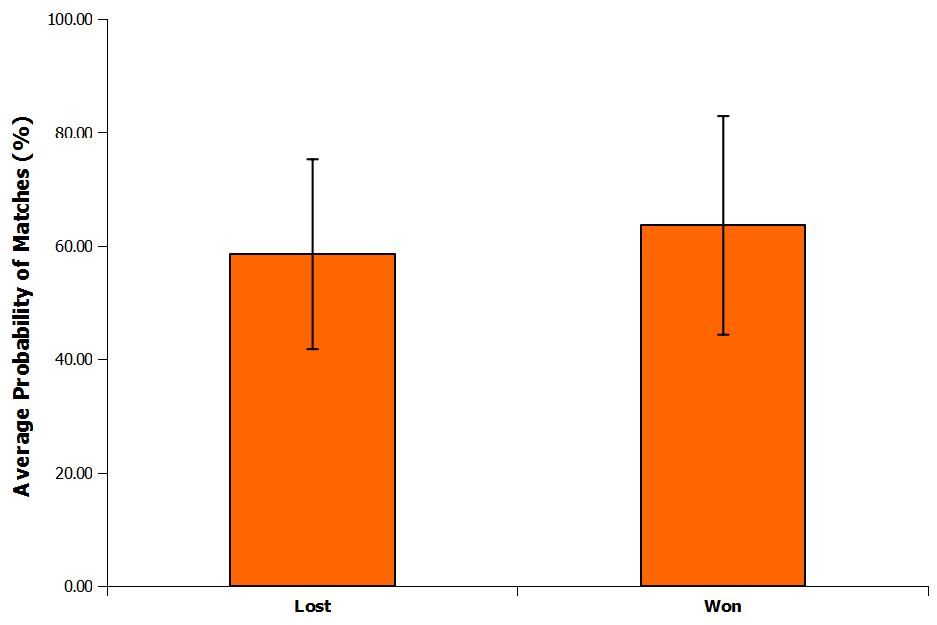
Figure 1: Average probabilities of matches correctly / incorrectly predicted by the Poisson model
Next I looked at which outcomes were being incorrectly predicted and a problem immediately became apparent. So far the model has predicted 50 matches of which 58% were predicted to be home wins, 34% as away wins and 8% as draws. Looking at what really happened though, of those 50 matches 42% were actually home wins, 30% away wins and 28% were draws (Figure 2). This suggests the model is under-predicting the likelihood of draws by quite a large margin and is actually predicting them as home wins.
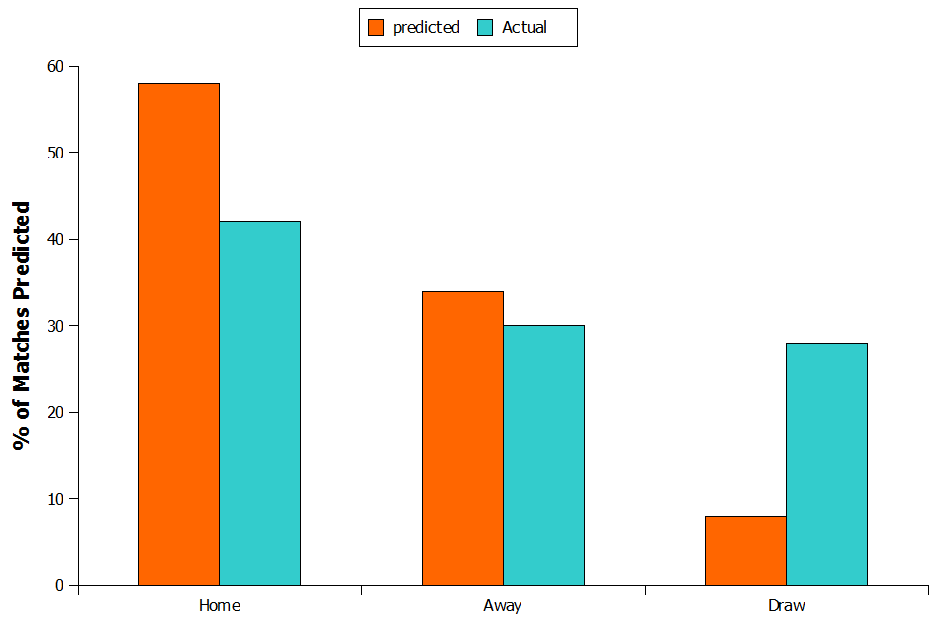
Figure 2: Proportion of Match Outcomes - Poisson vs Actual
Conclusions
A quick Google revealed two possible fixes. Karlis and Ntzoufras recommend replacing the independent Poisson with a bivariate Poisson to add an element of correlation between the home and away team’s scores. However, even with this they still needed to inflate the diagonal of the score matrix to try and improve the prediction of draws, suggesting that moving to the bivariate Poisson is not necessarily much of an improvement. An alternative proposal by Dixon and Coles was to stick with the two independent Poisson calculations but add in an additional parameter to modify the probabilities of 0-0, 1-1, 1-0 and 0-1 scores occurring.
So where does this leave the current Poisson model? For me, it is time to move on to other ideas. The Poisson model is one the most widely used models for predicting football outcomes so I will return to it in the future to try out the Karlis and Ntzoufras and Dixon and Coles adjustments but I gave a few other ideas to write about first.