Understanding Elo Ratings Part Two
Introduction
Now that we understand the theory behind Elo Ratings, let’s take a look at how to calculate them and how to make them more relevant to football.
Calculating Elo Ratings
The equation for calculating a team’s Elo rating is shown below in Figure 1, where $Ra_{new}$ is the team’s new Elo rating after a match, $Ra_{old}$ is the team’s previous Elo rating before the match and $k$ is a weighting factor. $Sa$ is the outcome of the match normalised to the range 0–1 so that 0 is a loss, 0.5 is a draw and 1 is a win.
$Ra_{new}=Ra_{old}+k(Sa-Ea)$
Figure 1: Elo Rating equation
$Ea$ is the expected probability of the team winning the match and is calculated using the equation in Figure 2 where $Rb-Ra$ is the difference in Elo ratings between the two teams.
$Ea=1/1+10^{(Rb-Ra)/400}$
Figure 2: Expected win probability equation
Win Expectancy
The calculation for $Ea$ is actually slightly different from the original Elo equation as it uses a logistic distribution for player performances rather than a normal distribution. The use of the logistic distribution stems the chess community, who suggested that it fit player performances better than the normal distribution did. In effect, the differences between the two are relatively minor, with the logistic curve skewing more performances to the tails of the distribution, meaning players are slightly more likely to over- or under-perform (Figure 3).
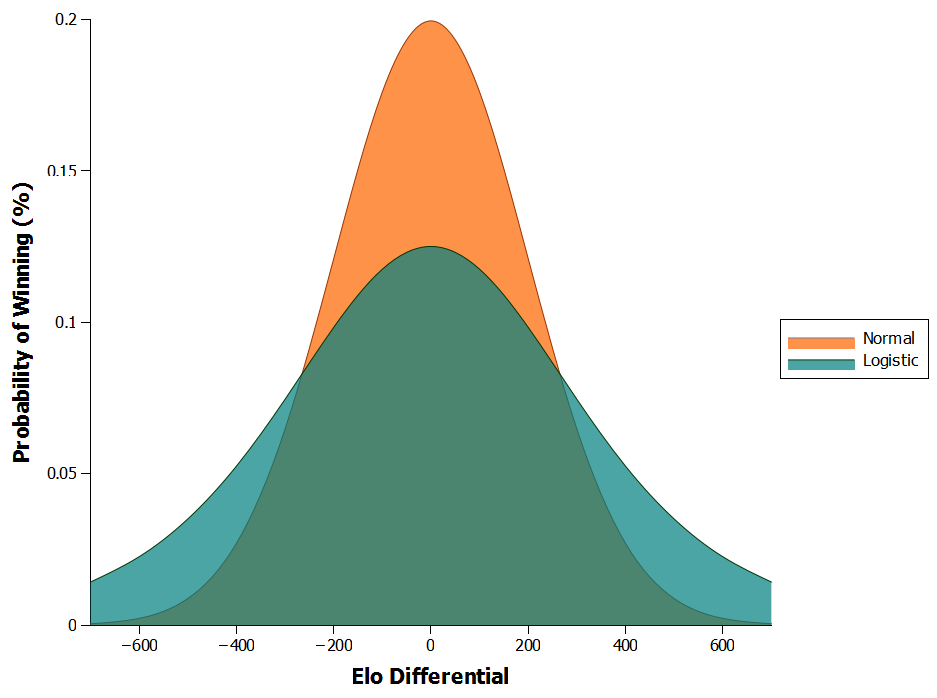
Figure 3: Comparison of logistic and normal distributions
Weighting Factor
The constant $k$ in the equation controls how many points are gained or lost each match. Increasing k will apply more weight to recent matches while lowering it will allow historic matches to have more of an effect on a team’s Elo rating. Therefore, using an inappropriate rating for $k$ may lead to inaccurate Elo ratings being calculated.
Eloratings.net is a website that applies Elo ratings to international football. They use a weighting of 60 for a world cup final, 50 for continental championship finals and major intercontinental tournaments, 40 for World Cup and continental qualifiers, 30 for all other tournament matches and 20 for international friendly matches. However, since none of these ratings apply directly to domestic football and since Eloratings.net does not explain how they were determined I decided to calculate my own.
Using Least Squares I optimized the value of $k$ to minimize the error of the predicted outcomes versus the actual match results using data from the English Premier League. Overall, the most accurate predictions were obtained using a value of 15 for $k$.
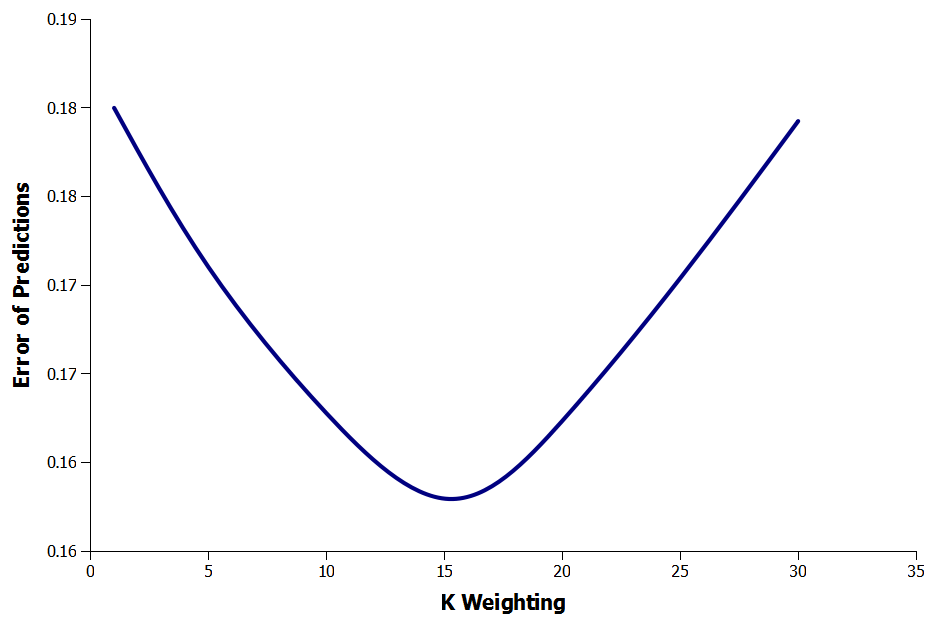
Figure 4: Effect of k on error of Elo prediction
Goal Difference
Another modification we can do to make the Elo ratings more applicable to football is to take into account the number of goals scored so that beating the opposition by two goals for example is better than wining by just one.
We can do this by scaling $k$ by the goal difference so that the larger the difference the more points are gained by the victor and the more lost by the loser. There are a number of ways this can be done but in my method each additional goal a team scores becomes increasingly less important. For example, going from 1–0 to 2–0 is much more critical in terms of winning a game than going from 8–0 to 9–0.
Eloratings.net used a similar approach where their scaling reduces the weightings for goal differences of two and three. However, for goal differences of four upwards their scale (intentionally or unintentionally) becomes linear and from then on applies equal weightings to each additional goal scored. Instead, I have used a sigmoid function to smoothly reduce the weightings of each goal scored to create the curve shown in Figure 5, which is then used to produce the scaling factors shown in Table 1
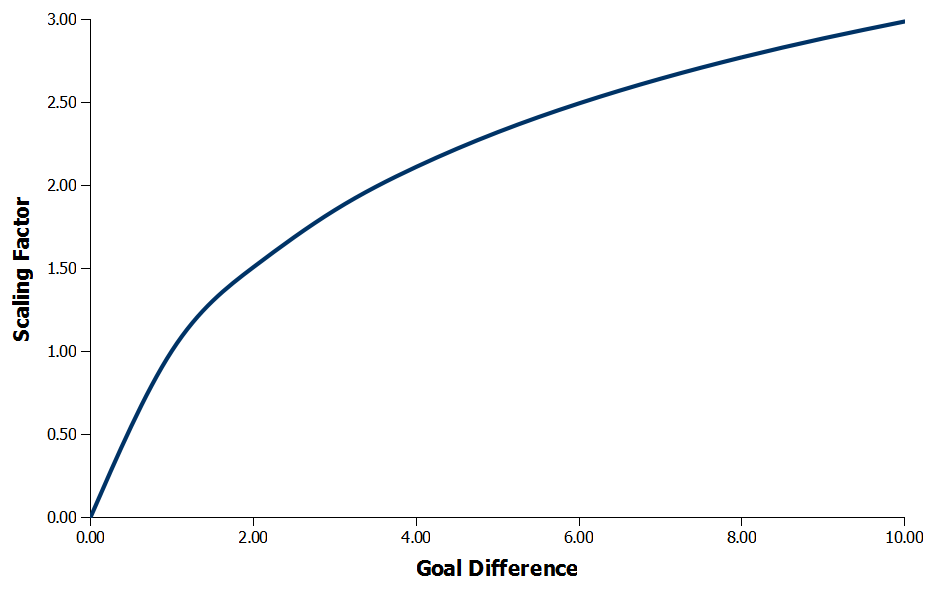
Figure 5: Goal difference scaling factor smoothed using a sigmoid
| Goal Difference | Scaling Factor |
| 10.00 | 2.99 |
| 9.00 | 2.88 |
| 8.00 | 2.77 |
| 7.00 | 2.64 |
| 6.00 | 2.49 |
| 5.00 | 2.32 |
| 4.00 | 2.11 |
| 3.00 | 1.85 |
| 2.00 | 1.51 |
| 1.00 | 1.00 |
Table 1: Goal difference scaling factors
Home Advantage
If two teams with equal Elo ratings play each other then in theory they should both have an identical chance of winning the match; however, in football the home team always has a noticeable advantage.
Looking back at the 2011–2012 English Premier League season, home wins accounted for 47% of results compared with just 24% for away wins. The remainder of the results are draws, which Elo ratings consider to be half a win, so including these gives us a final win expectancy of 61% for the home team and 39% for the away team.
To account for this we can give the home team’s Elo a temporary boost of 75 points. For two equally matched teams this then raises the win expectancy for the home team from 50% to 61%, matching what we see in the English Premier League.
Relegations and Promotions
Another issue to consider is how to deal with relegations and promotions. We could calculate Elo ratings for each tier of the league so that a team already has a rating when it gets promoted or alternatively we could award each promoted team the average Elo rating of 1500. A nice feature of Elo ratings is that they are self-correcting so although these arbitrary ratings may not be accurate they would gradually alter to the correct level.
This does have the unfortunate side effect of skewing the other team’s Elo values though. The gain and loss of Elo points is zero sum, meaning that for every Elo point a team gains another team has to lose one. So adding in teams with different Elo ratings would distort the values of other the team’s ratings by altering the overall number of points available in the league.
The simplest way to deal with this problem is to give the promoted teams the equivalent relegated team’s Elo rating. So the best promoted team takes the Elo rating of the best relegated team, the second best promoted team takes the Elo rating of the second best relegated team, and so on. This then keeps the correct number of Elo points in the league and maintains the parity in points between teams.
Conclusions
Elo ratings are a really quick and easy way to compare teams directly and calculate win expectancies. While techniques like the Pythagorean Expectation looks at how teams perform over a long period of time, Elo ratings can be used to look at teams on a match–by–match basis.
Comments
Lars - February 7, 2013
Thanks for this article.
I invite you to have a look at my website, where I am doing Elo ratings for European club football.
I lot of conclusions I have come to are similar to yours.
My least-squares curve for the weighting factor however looks a bit different, with a minimum at k=20 and not as symmetrical.
Glad to see that the Elo system becomes more and more popular.
Martin Eastwood - February 7, 2013
That is a really nice website Lars :)
It’s also good to see we have come to similar conclusions with regards to k factor etc.
Your use of the Poisson looks interesting too. I have played around with various Poisson models before but I have not tried combining it with the Elo before, an intriguing idea!
Stefan - February 7, 2013
Very interesting article, thanks!
I was wondering about two things:
1) In Figure 3, what are the parameters of the logistic distribution? Is it plotted for the same mean and variance as the normal distribution? Maybe this should be stated in the text.
2) What would happen if you used the actual match result, in particular the fraction of total goals scored, for “Ea” instead of just 0, 0.5, 1 for loss, draw, or win, respectively? For example, if the match ended 2-1, team 1 would have scored 66% of the goals, so the actual outcome would be 0.66 (and 0.33 for team 2). This would also naturally account for the weighting of goal differences, since the fraction of goals scored is much more similar when comparing 5-1 and 6-1 wins than for 2-1 and 3-1 wins. However, then one obviously has to deal with results where only one team scores and the outcome is always 100%/0% regardless of the goal difference.
I remember that the European eSports Leage ESL uses a similar ranking system for online games, see: http://www.esl.eu/eu/faq/rankmodules/ (interestingly also for the FIFA games^^) As far as I know, they added an offset of 1 to the match result, such that 1-0 is actually interpreted as 2-1, 2-0 as 3-1, and so on.
Martin Eastwood - February 7, 2013
1) Yes, the two distributions should be comparable with each other
2) That is a really interesting idea, I will have a play around with that and see if it works.
Thanks for the comments Stefan!
Stefan - February 7, 2013
If I had to guess, it could be that this underestimates the value of a close win (and I assume the majority of wins are with one goal difference). If this is the case you could play around with a sigmoid that pushes the actual match outcome away from 0.5 towards 0/1, but still allows for some gradual changes. Intuitively speaking, it should make sense to include the full information of the match score, which is more than just a ternary event (win, loss, or draw).
On a related note, it would be interesting to analyze whether the absolute goal difference or the goal ratio carries more predictive information.
Ian - September 2, 2013
Hi Martin, Can you please explain in layman’s terms how you calculated the optimal K value?
Same thing for the scaling factor – if it’s not too difficult.
Martin Eastwood - September 15, 2013
Most stats packages will have some sort of optimisation routines built in e.g optim in R or solver in Excel. These will iteratively work through a range if numbers looking to minimise or maximise some value for you. So for example you would look to minimise error or maximise likelihood to get the optimal value.
Ian - October 19, 2013
Thanks Martin, Just saw your reply now.
Can you (or Mick) run me through how to use solver to get the optimal K value? I’d really appreciate it.
Currently I’m regressing every team’s rating to the mean after each season. Would you guys recommend that I continue to do that after finding the optimal K value? Or would that become unnecessary?
Michael Podger - October 16, 2013
Hello Martin, great article
I analysed 4 years of A-League football (about 550 matches), using Solver to minimise the average error between the predicted and actual margin. The optimum K value was 75! Can you think of any reason why our K values would be so different ?
Thanks Mick
Martin Eastwood - October 16, 2013
Some leagues do seem to optimise to different k values. I found MLS to be quite different too due to its high level of parity so perhaps something similar with A league?
Mick Podger - October 18, 2013
Thanks Martin, thats probably it. A-league has a lot of equalisation measures which create more variability from year to year than you’d probably get in Premier League.
Nick - January 14, 2014
Hello. I don’t understand your probability formula. EA + EB = 1, but we have three possible results.
Martin Eastwood - January 20, 2014
Elo ratings only have two outcome – win and loss – so the draw probability gets merged between the two
Adam - April 12, 2014
I noticed that the Ea formula here is different from that in Wikipedia:
http://en.wikipedia.org/wiki/World_Football_Elo_Ratings
Any suggestions?
Martin Eastwood - April 12, 2014
If I remember correctly, my version is a modification to the original elo to use logistic regression to improve its accuracy a little bit more.
Adam - April 12, 2014
Thank you for your kind reply Martin! I’ve got another question if you do not mind.
Does Rb stands for the Away team and Ra for the Home team?
Martin Eastwood - April 12, 2014
No problem Adam, yes Rb should be the away team
Adam - April 12, 2014
Many thinks Martin!
Nathan Hause - August 12, 2014
First off I’d like to say great series of articles. I found them extremely helpful and surprisingly easy to understand.
I am commenting to inquire as to your success predicting wins/losses/draws with this model. After some minor tinkering with your Ea formula, some of the major statistics you outlined (home win %, away win %) and with some help from another site that had Elo ratings I was able to fashion together a prediction model. It was able to accurately predict the outcome for 11 of the final 14 matches in the EPL season including draws (I didn’t have enough data to go back further and test it). I am wondering if this a relatively high percentage or if you have been able to make a model that has more success.
Your input would be greatly appreciated, thanks.
Martin Eastwood - August 13, 2014
Hi Nathan – yes that looks a very high success rate! It’s a small sample size though so really you need to test it over more matches to see whether that level of accuracy is sustainable. Let me know how you get on with it :-)