Introducing the Eastwood Index
Introduction
My past couple of articles have focused on Elo ratings and how they can be applied to football teams to rank them against each other and to estimate win probabilities.
Problems with Elo Ratings
On the whole the Elo system works okay but it was not designed with football in mind and so there are some issues with it, for example it can only handle two distinct outcomes – winning and losing.
Elo ratings try to get around this problem by considering each draw to be half a win and half a loss. However, this means that the win probabilities calculated using the Elo equation are actually the probability of winning or drawing versus the probability of losing or drawing, which isn’t particularly useful.
For a game such as chess, which Elo ratings were originally developed for, this may not be too much of an issue as tied matches are comparatively rare but in football draws are a common occurrence so we really need to be able to model three outcomes – win, loss and draw.
The Eastwood Index
So instead of combining draws with wins and losses, we need to be able to calculate their probabilities individually. To do this I have been developing my own ranking system, which for want of a better name I am currently calling the Eastwood Index, or EI for short (it feels rather pretentious to be naming it after myself so if anyone has any better names for it then feel free to let me know!)
The Eastwood Index allows football teams to be ranked using a mathematical rating system that evaluates relative strength based on previous performances weighted so that more recent matches have a greater impact on a team’s ranking.
Methodology
Teams EI ratings are scaled so that the average rating is 2000. The higher the rating the better a team is compared with the rest of the league.
EI ratings increase when a team wins a match or draws against superior opposition. Conversely, EI ratings decrease when teams lose matches or draw against weaker opposition. The size of this increase or decrease in ratings is linked to the quality of the opposition. For example, beating a superior team is worth more than winning against a lower ranked team.
The change in EI rating is also weighted by the score line so that the greater the difference in goals scored or conceded then the greater the change in ratings. Home advantage is also included in the calculations so that the home team is considered to perform better at home compared with away.
So far this all sounds similar to an Elo rating. However, the Eastwood Index has a major advantage over Elo in that it is multinomial, meaning it can function with multiple outcomes. This makes it possible to accurately calculate the probabilities of teams winning, drawing or losing matches.
A further advantage of the Eastwood Index is that it is does not rely on the Logistic distribution the same way Elo ratings do. The use of the Logistic distribution in Elo ratings originates from chess where it was considered to predict chess outcomes reasonably well. Football and chess are different games with different outcomes so instead the Eastwood Index uses custom curves developed using football data. This means that predictions for football should be more accurate using the EI compared with Elo ratings.
Example
The underlying mathematics for the EI is completely different to how an Elo rating is calculated but rather than wade through a list of equations it is simpler to show how it works using the recent Liverpool versus Swansea match.
Prior to the game Liverpool had an EI rating of 2151 compared with Swansea’s rating of 1891. Team performances are considered to be normally distributed around their rating so on any given day a team may play above or below their true skill level. By comparing the distribution curves for the two teams we can then calculate the probabilities of each outcome of the match before it is played.
Although both teams have similar ratings Liverpool has the home advantage giving them overall a 52% chance of a win compared with a 25% chance of Swansea winning and a 23% chance of a draw (Figure 1).
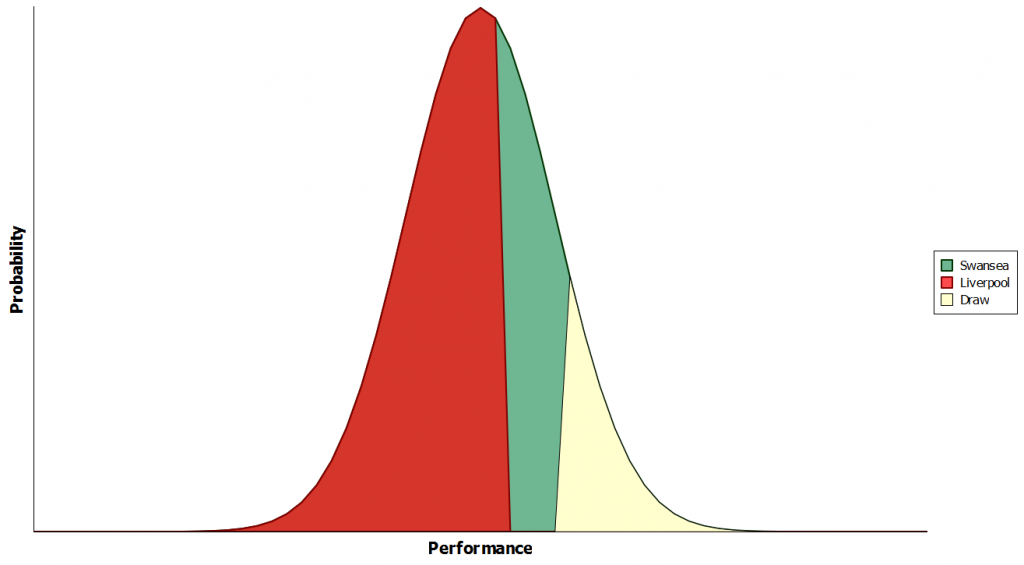
Figure 1: Predicting Liverpool Versus Swansea City
We can also use these probabilities to calculate the expected points from the match. If these two teams were to play the same match repeatedly then on average Liverpool would be expected to earn (0.52 * 3) + (0.23 * 1) = 1.79 points while Swansea would be expected to earn (0.25 * 3) + (0.23 * 1) = 0.98 points.
Once we know the actual result we can then update the EI for each team based on their current ratings and the score line, which was Liverpool 5 – 0 Swansea. Since Liverpool already had a higher EI rating and had beaten somewhat lesser opposition they would expect only a small rise in their EI but taking into account their high score in the match Liverpool’s rating moves up to 2183 while Swansea’s falls to 1859.
Conclusions
The EI Index offers a potentially superior way of rating football teams compared with other ranking systems, with the advantage that it can predict wins, losses and draws, and uses mathematics specifically designed to accurately model football data.
I will be discussing the EI in more detail in future posts and showing how it can be used to analyse and predict football matches.
As ever, get in touch if you have any comments of questions!
Comments
Lars - February 21, 2013
Hello Martin,
I admire the courage to come up with a completely new ranking system. There are a lot of things to be taken into consideration if you want to set up a solid theoretic basis for such a complex problem. That is why I shy away from developing something completely new and rather stick to Elo, certainly not perfect but still very good in my eyes.
Please tell us more about the maths behind it so that substantiated comments are possible. Until then, let me give you my first thoughts I had when reading this:
1) It seems that by using the 3-point rule for the ranking, you leave the ground of zero-sum-games. This would imply that two teams can increase (or decrease) their average ranking just by playing each other. I wonder if that is intended?
2) If you do not want to be pretentious, name it after what it does or its unique feature (multinomial or whatever).
Martin Eastwood - February 21, 2013
Hi Lars,
Yes Elo is certainly adequate and I am not trying to criticize it. Rather I am just trying to improve things further although I am sure there is still more to do as this is just the first version of the system. In answer to your questions:
1) The mathematics is designed to ensure the system is zero-sum so the average rating for the league will always be 2000
2) perhaps the Multinomial Football Index? I may just stick with EI and then just avoid referring to what the E stands for :)
Rob - February 21, 2013
Hi Martin
Enjoy your blogs and find them very interesting .
Just trying to get my head around your example of Liverpool v Swansea. If I am correct then you award extra points for a 5-0 win (goals) but Swansea had rested the majority of the team if memory serves me correctly so could you take that into account when awarding points or is Subjectivity a dangerous state to avoid when putting together ratings ?
Martin Eastwood - February 21, 2013
Thanks Rob. At the moment it is based purely on the actual match result, so far I haven’t found a good way to quantify whether a team has put out a weakened squad for a match.
Baloo - February 21, 2013
I use a similar rating system (purely to assess opposition strength) and if I had a team rated 250 points higher, it would mean they are around 1.25 goal favourites. Add on home advantage and you get Liverpool in at 1.65 goal jollies (ie roughly 73.5% to win the game).
My pricing method is a lot more complicated but I also had Liverpool around 1.65 goal favourites and bet accordingly.
How did you get to 52%?
Martin Eastwood - February 22, 2013
The 52% is based on the difference between the two team’s performance distribution curves. For such closely matched teams though 73.5% sounds slightly high?
Baloo - February 22, 2013
What do you mean by performance distribution?
I would strongly disagree that they are closely matched on performance (or even just shot) data, which is essentially what drives the betting markets. They are closely matched only in pure results terms.
Liverpool continually divide opinion however, and I have to admit I’m in the minority when it comes to rating them.
They are an outlier, just as Man Utd are also an outlier but at the opposite end of the spectrum.
Martin Eastwood - February 22, 2013
The model considers individual performances to be distributed around the team’s current EI rating. Yes Liverpool are quite a controversial team to rate, personally I never think the odds for them look how I would expect them to. I agree about Man Utd they are a huge outlier this season and based on many of their individual stats they would not be expected to be where they are.
Vasilis - August 30, 2013
Hi, I have a question. At the beginning of a season, so you make and a subjective evaluation of all teams, do you start all teams with 2000 points, do you rely on last years ranking to handicap better teams? And once the start up points have been awarded, does your system takes into account purely results, or do you feed it with subjective criteria as well?
Martin Eastwood - August 30, 2013
All teams initially started off equal on 2000 points. Promoted teams them take over the equivalent relegated team’s rating and other team’s ratings carry over from one season to the next. At the moment it is based purely on results but at some point I plan to investigate whether subjective criteria can help account for changes e.g.manager changes / transfers / summer breaks etc.
Vasilis - August 30, 2013
Nevertheless, dont you think that not all teams have the same probability of winning the trophy? I mean, if you figured out a way to evaluate odds for each team winning the 1st place, and then compiled them around 2000, but with weights in order to have a more realistic initial point, wouldn’t that be more accurate? Also, does your model take into account the total number of teams participating in the league. I mean, do you use the 2000 initial points for Scottish Premier league (12 teams), and for England Premier (20 teams)too? I guess that a team loosing all matched would have its points limit close to zero, but not negative, correct? Hence the 2000 points shouldn’t be adjustable to each league?
Martin Eastwood - August 30, 2013
When I initially set up the model I ran it over the three previous season’s data so that all teams ratings had time to move from the 2000 to the correct value to represent the team’s values so no need to weight them.
The effect of league sizes is something that intrigues me as ideally I would like to run the model over multiple leagues and seasons and have ratings comparable between them all so some form of weighting will be required, although I am not sure of the best solution though. Still trying to find an answer that I am happy with.
Nick - April 16, 2014
EI is great but your statement that draws in chess are relatively rare is not correct. “For a game such as chess, which Elo ratings were originally developed for, this may not be too much of an issue as tied matches are comparatively rare but in football draws are a common occurrence” Actually, quite the opposite – no other game has as high ratio of draws as chess, over 50% of chess games played at high (professional) level are drawn. https://en.wikipedia.org/wiki/Draw_(chess)#Frequency_of_draws
Martin Eastwood - April 16, 2014
I stand corrected Nick :-)
Johan - April 23, 2014
Hi Martin.
I’m relatively new to your blog but reading a new article every morning on my way to work. Interesting content (and comments).
Your system the EI index sounds somewhat similar to Paul Steele’s power ratings. Would you mind sharing the formula (like Steele) so it’s possible to compare their performance on the same data sets?
I found Mr. Steele’s system to work quite well especially for Home wins (roughly 66% correct) but it would be good fun if there was a system that could beat it especially on away wins (roughly 40%).
I can send you his formula if you like (pls advise me of your email).
Best regards,
Johan
http://google.com/ - June 14, 2014
whoah this weblog is fantastic i like studying your posts.
Keep up the great work! You already know, a lot of individuals are hunting around for this information, you can help them greatly.
Empecinator - July 7, 2014
Hi Martin,
Thanks for the blog as it is very interesting and easy to read. However and same as Baloo I don’t see how you get to the 52% chance of victory for L’pool, i.e. how to you infer the multinominal probabilities from the Win-Lose calculated with the Ea logistic formula (explained in a previous article)?
I understand it can be calculated from the overlay distributions but will you (or have you) publish it?
Cheers
Martin Eastwood - July 12, 2014
Hi Juan,
I’ve moved away from the EI as I couldn’t find a good way of forecasting scores from it so while it worked well for 1X2 probabilities it was not much use for Asian handicaps. It’s unlikely I’ll bother publishing it now since I no longer use it or keep it up to date.