How Accurate Are The EI Football Predictions?
Introduction
Unfortunately time caught up with me last week and I was unable to post any predictions from my Eastwood Index. However, since then I have been busy validating the results to see how accurate the predictions really are using the 296 matches played in the English Premier League so far this season.
Ranked Probability Scores
I have previously discussed the problems of trying to determine the accuracy of probability-based models and Jonas posted a suggestion in the comments section recommending the use of ranked probability scores, which turned out to be a really interesting idea.
Ranked probability scores were originally proposed by Epstein back in 1969 as a way to compare probabilistic forecasts against categorical data. Their main advantage over other techniques is that as well as looking at accuracy, they also account for distance in the predictions e.g. how far out inaccurate predictions are from what actually happened.
They are also easy to calculate. The equation for ranked probability scores is shown in Figure 1 for those of a mathematical disposition, where $K$ is the number of possible outcomes, and $CDF_{fc}$ and $CDF_{obs}$ are the predictions and observations for prediction $k$.
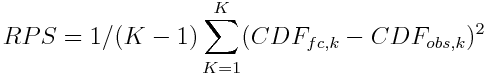
Interpreting Ranked Probability Scores
Ranked probability scores range between 0–1 and are negatively orientated meaning that the lower the result the better. For simplicity, you can think of them representing the amount of error in the predictions where a score of zero means your predictions are perfect.
The Results
I started off looking at how well I would have done if I had just guessed at random for each match in the English Premier League this season rather than using the Eastwood Index and obtained a ranked probability score of 0.231.
Next, I looked at how well the bookmaker’s odds predicted matches. To do this I aggregated the odds from multiple bookmakers, partly to reduce the comparisons needed and partly because aggregating data often improve predictions and I wanted to give the Eastwood Index the toughest test possible. This gave a ranked probability score of 0.193 for the bookmakers.
Finally I calculated the score for the Eastwood Index and got…
drum roll please
a ranked probability score of 0.191. Okay, it is not much lower than the bookmakers but it does mean that so far this season the Eastwood Index has been more accurate at predicting football matches than the combined odds of the gaming industry which is really pleasing for me.
Conclusions
Most importantly though this suggests that the Eastwood Index works. I had originally set myself the target of being able to compete with the bookmakers as I consider them to be gold standard prediction for football. These are large companies employing professional odds compilers to generate their odds so for me to be able to beat them, even by a small amount, using a bunch of equations is a big success for the Eastwood Index.
It is still early days and it is still a relatively small number of predictions (n=296) so I will be continuing to monitor the results to check the accuracy doesn’t change over time. It is a fantastic start though and great inspiration to continue developing and improving the Eastwood Index further!
Comments
amir - March 23, 2013
Have you calculated the RPS for the same 296 matches for the bookmakers too? Otherwise, you put them at disadvantage to begin with, as early matches are harder to predict. Also, have you used the data from this year’s EPL to improve the EI. If you did, you probably did over-fitting…
Martin Eastwood - March 23, 2013
Hi Amir
EI and bookmaker’s RPS was tested using exactly same set of matches.
The EI was developed using historical data from the EPL rather than relying on this season’s data to prevent overfitting model.
Thanks for leaving your comment.
amir - March 23, 2013
The results are very impressive then.
Looking forward to read more details about the EI methodology!
Martin Eastwood - March 23, 2013
Thanks!
Lars - January 20, 2014
The Ranked Probability Scores method looks straightforward and really meaningful.
Thanks for bringing it up, I plan to use it myself, too.
Martin Eastwood - January 20, 2014
Yes, it’s a great way to measure accuracy. I’m using it more and more for assessing football models now.
Lars - January 28, 2014
I have worked my way through Epstein’s paper now, a few comments:
Contrary to what is written here, a high RPS is good, not bad. Even without understanding the equations, you can see in the table 2 on page 987 of the paper that the score is 1 when the prediction is correct and is <1 the worse the prediction is.
Secondly, I have tried to work out where you get the simplified equation from that you show above.
In my eyes, for football (3-way result) it should rather be:
RPS = S – 0.5 * (P_d+2*P_a) in case of home win
RPS = S – 0.5 * (P_h+P_a) in case of draw
RPS = S – 0.5 * (2*P_h+P_d) in case of away win
where:
S = 1.5 – 0.25*(P²_h +(P_h+P_d)²+ (P_d+P_a)²+P²_a )
and:
P_h is the probability for a home win, P_d for a draw and P_a for an away win.
Maybe this can be corrected above or let me know where I am wrong.
Martin Eastwood - January 29, 2014
Perhaps the Epstein paper doesn’t make it particularly clear but the RPS is the sum of the squared differences between the forecast and observation. Therefore the more accurate the forecast then the smaller the difference is and the lower the RPS.
If you are interested in digging deeper into RPS then this book has quite a good chapter on it IIRC – http://www.amazon.co.uk/Statistical-Atmospheric-Sciences-International-Geophysics/dp/0123850223/ref=tmm_hrd_title_0?ie=UTF8&qid=1390988812&sr=8-2-fkmr0
Lars - January 29, 2014
I disagree. The “sum of the squared differences between the forecast and observation” does not take into account the ranking characteristic. And your formula from above does not either.
There would really be no reason to call it RPS if it was just a sum of squared differences.
What Epstein does makes sense and is clearly different. And I did not find that the paper leaves open questions or was not particularly clear.
Martin Eastwood - January 29, 2014
Have you checked whether Epstein have an additional 1- term in his paper because RPS typically ranges from 0-1, with 0 considered the perfect score. Or perhaps you’re looking at Ranked Probability Skill Scores where higher values are better?
Lars - January 29, 2014
Whether 0 or 1 is defined as perfect is a minor issue. It is more where the “ranked” comes in.
For that I have found on google a site that uses the same formula as you:
http://www.eumetcal.org/resources/ukmeteocal/verification/www/english/msg/ver_prob_forec/uos2b/uos2b_ko1.htm
And they add to their description that CDF is the CUMULATIVE distribution.
Now that makes more sense and I think you probably do the same it is just not mentioned above. I did not get this the whole time.
I see now why you do it and why it is called RPS. That’s fine.
Epstein still does something different though (see my comment above where I apply Epstein to football).
Martin Eastwood - January 29, 2014
Thanks Lars
Adam - March 17, 2014
Hi Martin,
Have you ever used the Ranked Probability Skill Score to evaluate your model rather than just the RPS? I’ve been using the RPS however I’ve seen on sites discussing probabilistic forecast verification, a mention of the RPSS, but i’m unsure as to how to apply it to football predictions. It compares the forecast to a ‘reference forecast’, and I’m wondering what the equivalent is in football (a sample climatology is the example given for weather forecasting). It’s defined here: http://www.cawcr.gov.au/projects/EPSverif/scores/scores.html
Cheers,
Adam.
Martin Eastwood - March 17, 2014
Hi Adam,
I’ve never tried the RPSS, perhaps you could use aggregated bookmaker odds as the ‘reference’ and compare against that?
Thanks
Martin
Ian - March 27, 2014
Hi Martin,
Just wanted to make sure I understand, is CDFfc, effectively your estimated probability of said outcome? As such, in a match where a bookmaker offered 1/2 on a team to win, this would be 0.67? Then the CDFobs would be either 0 or 1?
Am I right in thinking that therefore in theory, a coin toss prediction, where the prediction of 50% is in fact the perfect probability, would have an RPS of approximately 0.25?
Also, any idea why it divides by (K-1) rather than just K?
Cheers,
Ian
Ian - July 11, 2014
Hi Martin,
Did you have any thoughts on what I asked above?
Sorry to persist,
Ian
Martin Eastwood - July 12, 2014
Apologies Ian, I completely missed your comment.
In terms of the coin toss you wouldn’t use RPS as it is intended for when there are more than two possible outcomes. Instead, you would use Brier Scores which is effectively the same thing but for situations with two outcomes, giving the mean squared error of the forecasts. And yes, for the coin toss example you would expect a Brier Score of 0.25.
Not sure about the k-1 part, I’d have to go back and look at Epstein’s paper. I’ve not read it for a while..
Thomas - July 27, 2014
Hi Martin,
Why are your values so constant after the first matches? I would expect to see a spike for those matches where an underdog wins?
Bests and thanks for the great work,
Thomas
Thomas - July 27, 2014
Sorry the comment was indented for post: http://pena.lt/y/2013/05/21/did-the-eastwood-index-beat-the-bookmakers/
Martin Eastwood - July 27, 2014
It’s the average rps of all the forecasts so individual matches tend not to cause spikes due to the smoothing from the aggregation.