Massey Ratings For Football Part Two
Introduction
In part one I introduced Massey Ratings and how they can be used to rank football teams in a way that accounts for their strength of schedule. Next, we’ll take a look at how Massey Ratings can be extended further to look at team’s attack and defence strength separately.
Massey Ratings
The idea behind Massey Ratings is that they rate teams such that the difference between any two teams is equal to the expected margin of victory between them. For example, if a team rated -1.0 played a team rated +1.0 then we’d expect the average goal difference between them to be two goals.
Since Massey Ratings look at goal difference rather than goals scored or conceded they account for a team’s overall strength and combine both their attack and defence strengths together into a single value. This means with a bit of mathematics we should be able to decompose a Massey Rating to split out these two constituent parts.
Attack And Defence
In part One we originally defined the Massey Rating as shown below in Equation One:
$y=ra–rb$
where y is the margin of victory for fixture, ra is the rating of team a and rb is the rating of team b. Let’s take this a step further and define the total goals a team should score in a match as Equation Two below:
$ya=oa–db$
where ya is the number of goals team a is expected to score, oa is team a’s attack strength and db is team b’s defence strength.
Extending this further we can say the total goals a given team should score over the course of a season is therefore equal to its attack strength multiplied by the number of matches played minus the sum of the defence strength of all its opponents. Since we know what the team’s overall rating are, how many matches they’ve played, how many goals were scored and who their opponents were we’re getting pretty close to getting what we need.
Decompose The Massey Matrix
Next we need to decompose the Massey Matrix we created in Part One into it’s diagonal and off-diagonal elements to give us two new matrices, G and P, which we use in Equation Three below:
$(G–P)r=p$
where G is total games played, P is the number of pairwise matchups each team has played, r are the team’s Massey Ratings and p is a vector of the team’s goal differentials.
From here, Ken Massey uses some clever algebra to derive the equivalent of Equation Four below:
$(G+P)d=Gr–f$
where G is total games played, P is the number of pairwise matchups each team has played, d is the defensive rating and f is the number of goals scored.
If you are interested in finding out more about the mathematics behind this then I heartily recommend taking a look through Ken Massey’s thesis where he explains it in much more detail than I’ve gone in to here.
Calculating The Ratings
Finally, we can now solve this linear system to get the attack and defence ratings for each team.
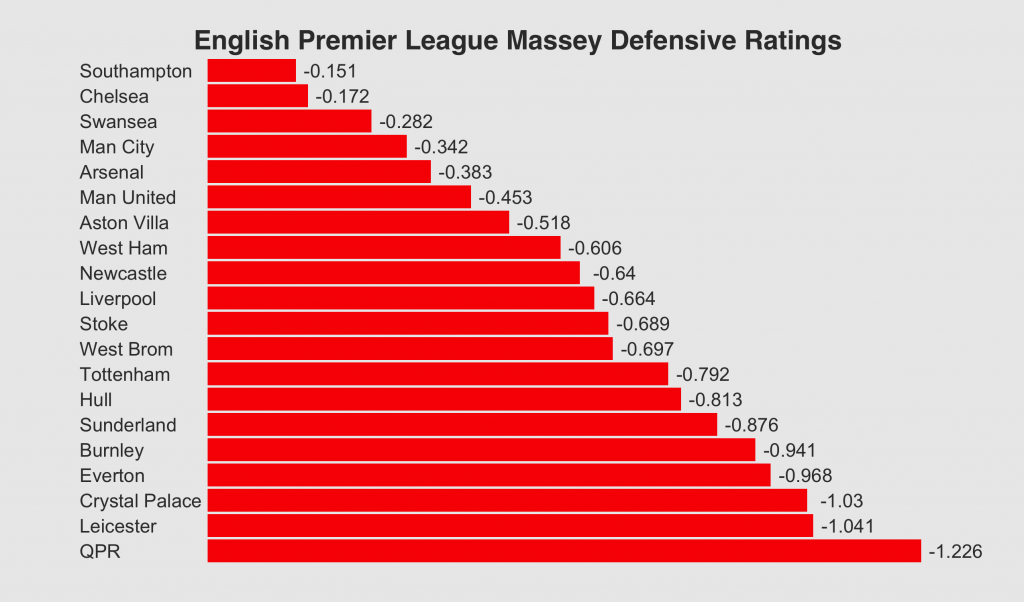Figure One: Defensive Massey Ratings
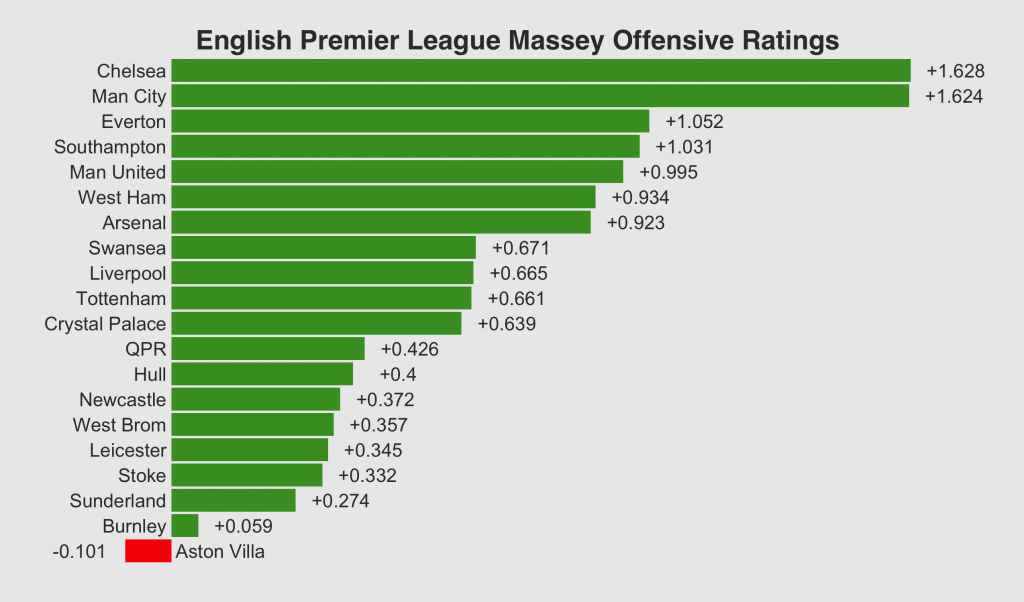Figure Two: Offensive Massey Ratings
It’s no surprise that Manchester City and Chelsea rate high for offensive strength but Everton are somewhat surprisingly rated third best offensive team even though they only rank mid-table in the league. Everton may only have a goal difference of +2 at the moment though but they are actually joint third highest goal scorers in the Premier League. They are performing well offensively, it’s their defence that is letting them down and is actually ranked worse than relegation-threatened Burnley’s.
QPR also rate pretty high in terms of attacking strength for a team in the relegation zone. Looking at their results for this season though they managed to score two against Manchester City, scored against Chelsea and are one of the few teams to actually get a goal against Southampton so they are performing well offensively against the league’s stronger teams. Like Everton though, their defence is performing poorly and dragging down their overall performance.
What’s that at the bottom of the offensive chart in red? Why it’s Aston Villa whose attack is so poor it actually gets a negative rating! I’ve mentioned in my last two articles about how Aston Villa’s Pythagorean and Massey Ratings show them to be seriously over-placed in the league and once again here’s another metric showing how poor they are. Bizarrely, Villa are somehow in twelfth place having managed a pitiful eight goals from fourteen matches. Although they are mid-table in the league and their defensive rating is pretty good, from an offensive point of view Aston Villa’s numbers suggest they are perhaps rather fortuitous to be so far away from the relegation zone…
Further Improvements
So far the Massey Ratings have considered each match a team plays equally but Ken Massey suggests they can be improved further by weighting matches based on their importance. For example, playing a cup match against a team from a lower division is probably less relevant to calculating the ratings than say a league match against a close rival. By weighting matches appropriately we can reduce the influence less relevant matches have on a team’s ratings and potentially improve their accuracy.
Example Code
If you are interested in having a go with Massey Ratings then I’ve put some example R code on GitHub. You’ll need to add your own data though as I’ve stripped out the section where it connects to my database for security reasons.
Comments
Peter - December 4, 2014
Great read as always.
Currently in the process of teaching myself R. Just wondering if you could give me a pointer as I’m really interested in giving this a go! What headers should the data be ordered in? Is this all taken from a league table, or from the results csv on the football-data website?
Cheers,
Peter
Martin Eastwood - December 5, 2014
It was all taken from my PostgreSQL database so you’ll need to make sure your data matches the naming conventions used in the code or change the code to match your data.
Kevin - December 5, 2014
Have you thought about improving the ratings by using expected goals, rather than goals, in your matrices?
Martin Eastwood - December 5, 2014
Not tried, but it’s an interesting idea!
Peter - December 8, 2014
Hi Martin,
I have given it a go (through Excel, not R) and while I have taken a different approach, things seem to look fairly consistent regarding the overall ratings. I’ll cautiously refer to it as an Adjusted Massey… I’m thinking decomposing these attack/defense ratings may prove a challenge however. I’m using it in conjunction with Pythagorean Expectation to gauge overall performance, and will have a blog post up fairly soon (with due reference to pena.lt/y/ for lighting the way of course)!
Cheers,
Peter
Martin Eastwood - December 9, 2014
Cool, look forward to reading it Peter!