Using the Pythagorean Expectation Across Leagues Wordwide
Introduction
I showed in my last post that my initial version of the Pythagorean Expectation (MPE) predicted total points for the English Premier League (EPL) pretty well, with an RMSE of approximately four points over the course of a whole season (see here for an explanation of using RMSE to measure the error of the predictions). The next stage for the equation’s development is to see whether it can be applied to other leagues too. Having one MPE equation that could be used globally across leagues is preferable to having to create specific equations for each league.
The Eredivisie
At the recommendation of Scoreboard Journalism's Simon Gleave I started with the Eredivisie, the top flight division in Holland. The reason for choosing the Eredivisie is that it is a unique league, with high rates of goal scoring and a number of results in recent years that appear as potential outliers. For example, in the 2009–2010 season Ajax scored 43 goals more than Twente and conceded three fewer yet still finished second to them in the league. At the other end of the table Willem II finished 15th in 2007–2008 with a goal difference of -9 while the two teams immediately above them had goal differences of -30 and -24, respectively. These sort of results make the Eredivisie difficult to predict and so provide a good stress test for the MPE equation.
Applying the MPE to the final Eredivise standings from 1999–2000 to 2011–2012 worked surprisingly well, with an overall RMSE of 4.35 points. It is slightly higher than the 4.08 previously obtained for the EPL but this is perhaps to be expected since the original MPE equation was generated using just data from the EPL.
To see whether the Dutch league needed its own version of MPE I recreated the equation based on just Eredivisie data and the overall error dropped to 4.21, a decrease of around 3%. Such a minor improvement suggests that the equation maybe stable across leagues and so we will not need league-specific versions.
To test this hypothesis further I collected 223 league tables from around the world and optimised the MPE against this larger data set. The reason for this was three-fold. Firstly, the original equation I published was created just from EPL data so any peculiarities to the EPL could bias results for other leagues.
Secondly, the previous data set was smaller so any outliers in the data could have a large effect on the finalised results. By using a larger data set the influence of any outliers will be minimised.
Thirdly, and perhaps most importantly, this gave enough data to cross-validate the equation by randomly splitting the league tables up into training and validation sets. Initially, the MPE had been trained and tested using the same data. Now it has been tested on different data to which it was optimised against, reducing the risk of Type III errors errors occurring.
Figure One shows the RMSE for the predictions for fifteen leagues randomly selected as a validation set. The overall RMSE across the entire validation set is 3.88 points and is plotted as the vertical dotted line. The overall RMSE is now reduced to below four points and this new version of the MPE equation appears suitable for use globally across different leagues.
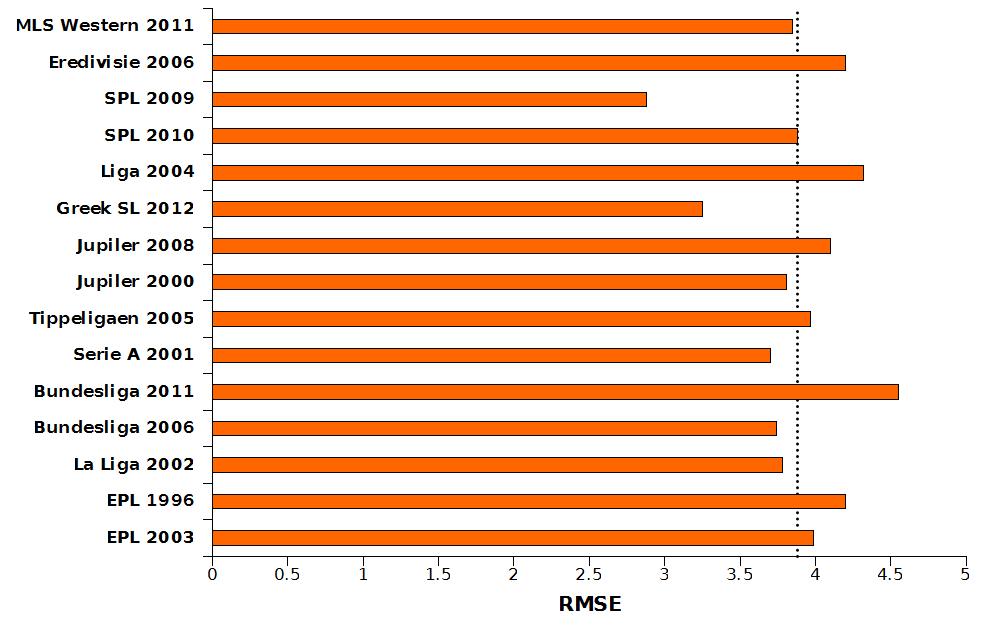
Figure 1: Results For Validation of MPE Equation
The finalised MPE Pythagorean Expectation is shown in Figure 2. Based on the data shown here this new version of the MPE equation is suitable for use across multiple leagues worldwide, with an average error of less than 4 points per season.
$predicted points = (goalsfor^{1.2299}/(goalsfor^{1.16793} + goalsaway^{1.20053})) * 2.29761 * numberofgamesplayed$
Figure 3: MPE Equation