Estimating Goal Expectancy From Bookmaker's Odds
Introduction
I've explored lots of different ways of predicting football matches so far on this blog that have all been backwards looking - they take in historical data and try and use it to predict how many goals will be scored.
This goal expectancy is then used to work out the probabilities for the match, e.g. what's the probability the home team wins, or that it's a draw, what are the prices for the over / under markets etc.
This time we're going to do things the opposite way round and use the bookmaker's odds to predict goal expectancy.
Data
Let's start off by getting some bookmaker's odds from football-data.co.uk. This is really easy to do using the scraper from the penaltyblog python package, which can be installed via pip if you don't already have it.
One we have the data, we filter out the columns we don't need to make it a little easier to work with. The psh, psd and psa columns represent Pinnacle's home, draw and away odds for each fixture.
import penaltyblog as pb
df = pb.scrapers.FootballData("ENG Premier League", "2022-2023").get_fixtures()
cols = [
"date",
"team_home",
"team_away",
"goals_home",
"goals_away",
"psh",
"psd",
"psa",
]
df = df[cols]
print(df.head(5))
| date | team_home | team_away | goals_home | goals_away | psh | psd | psa |
|---|---|---|---|---|---|---|---|
| 2022-08-05 | Crystal Palace | Arsenal | 0 | 2 | 4.50 | 3.65 | 1.89 |
| 2022-08-06 | Bournemouth | Aston Villa | 2 | 0 | 3.93 | 3.58 | 2.04 |
| 2022-08-06 | Everton | Chelsea | 0 | 1 | 6.04 | 4.06 | 1.63 |
| 2022-08-06 | Fulham | Liverpool | 2 | 2 | 11.20 | 6.22 | 1.28 |
| 2022-08-06 | Leeds | Wolves | 2 | 1 | 2.39 | 3.33 | 3.30 |
The Overround
The odds in the psh, psd and psa columns are currently in decimal notation. Let's take the first fixture as an example and convert the odds into probabilities instead by taking the reciprocal.
example = df.iloc[0].copy()
example["psh"] = 1.0 / example["psh"]
example["psd"] = 1.0 / example["psd"]
example["psa"] = 1.0 / example["psa"]
print(example)
| date | 2022-08-05 00:00:00 |
|---|---|
| team_home | Crystal Palace |
| team_away | Arsenal |
| goals_home | 0 |
| goals_away | 2 |
| psh | 0.222222 |
| psd | 0.273973 |
| psa | 0.529101 |
Hmmm, something's not right here. Our fixture only has three possible outcomes (either the home team wins, the away team wins or it's a draw) so the probabilities should add up nicely to 1.0 but example["psh"] + example["psd"] + example["psa"] adds up to 1.025. Somehow, we're out by 2.5%.
The reason is the overround - this is an extra bit of margin the bookmaker has factored into the odds to help guarantee them a profit regardless of the fixture's outcome.
There are a whole load of different ways we can try and remove this overround and get back to the original odds before the bookmaker skewed them in their favour. We're going to use the power method included in the penaltyblog package.
import pandas as pd
def overround(row):
odds = [
row["psh"],
row["psd"],
row["psa"],
]
odds = pb.implied.power(odds)
return pd.Series(odds["implied_probabilities"])
df[["psh", "psd", "psa"]] = df.apply(overround, axis=1)
print(df.head())
| date | team_home | team_away | goals_home | goals_away | psh | psd | psa |
|---|---|---|---|---|---|---|---|
| 2022-08-05 | Crystal Palace | Arsenal | 0 | 2 | 0.214017 | 0.265241 | 0.520742 |
| 2022-08-06 | Bournemouth | Aston Villa | 2 | 0 | 0.246553 | 0.271239 | 0.482208 |
| 2022-08-06 | Everton | Chelsea | 0 | 1 | 0.157612 | 0.237040 | 0.605349 |
| 2022-08-06 | Fulham | Liverpool | 2 | 2 | 0.079856 | 0.147753 | 0.772391 |
| 2022-08-06 | Leeds | Wolves | 2 | 1 | 0.411107 | 0.293087 | 0.295806 |
Brilliant, we've now got the implied probabilities for the each fixture without the overround messing them up.
Goal Expectancy
Now we've got the data we need, how do we convert it into goal expectancies?
If you remember back to previous articles, we used the predicted number of goals to work out the probabilities for a home win, away win or a draw occurring.
This time though, we've got the probabilities for the outcomes but not for the goals scored. So, in theory all we need to do is try different combinations of home and away goals to see which ones give us those probabilities back.
We could do this through brute force by trying lots and lots of different score lines but that's slow and tedious so we're going to use scipy's minimizer to speed things up.
Instead of randomly trying lots of score lines, scipy will look at the error between our guesses versus the bookmaker's probabilities to work out what score lines to try out next and hopefully find us the answer more quickly.
To do this, we're going to need a function to measure the error between us and the bookmakers. We're going to use something called Mean Squared Error (MSE) as shown below.
from scipy.stats import poisson
import numpy as np
def _mse(params, home, draw, away):
exp_params = np.exp(params)
mu1 = poisson(exp_params[0]).pmf(np.arange(0, 16))
mu2 = poisson(exp_params[1]).pmf(np.arange(0, 16))
mat = np.outer(mu1, mu2)
pred = np.array([
np.sum(np.tril(mat, -1)), # home
np.sum(np.diag(mat)), # draw
np.sum(np.triu(mat, 1))]) # away
obs = np.array([home, draw, away])
mse = np.mean((pred - obs)**2)
return mse
The _mse function takes an argument called params, which is the home and away goals to test and then exponentiates them. These values are then plugged into a Poisson distribution to get the probabilities for each team scoring 0-15 goals. We then take the outer product of these two sets of probabilities to get a matrix giving the probability of each possible scoreline.
This matrix is a bit like a spreadsheet, so in the example below we have a probability of 0.01041474 for nil-nil, 0.1207623 for 3-0, 0.00436915 for 1-2 and so on.
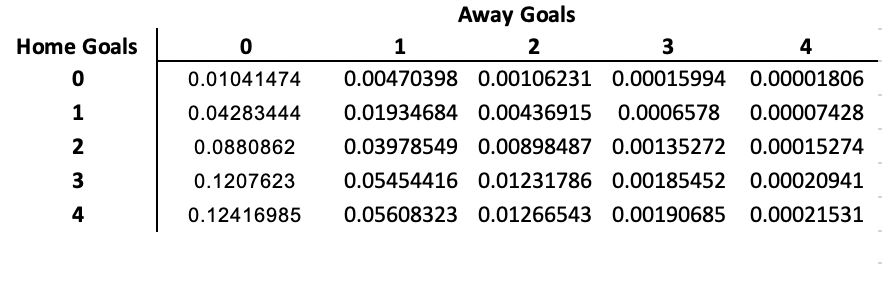
The sum of all the probabilities on the diagonal of this matrix gives us the overall probability of a draw, the sum of all the probabilities above the diagonal is the probability of an away win and the sum of all the probabilities below the diagonal is the probability of a home win.
We then just take the difference between our estimated probabilities and the bookmaker's probabilities, square them (to ensure they are not negative) and return the average back to the minimizer.
The job of the minimizer is then to find out what combination of expected home and away goals returns the lowest error. Let's set up the minimizer next.
from scipy.optimize import minimize
def goal_expectation(home, draw, away):
options = {
"maxiter": 1000,
"disp": False,
}
res = minimize(
fun=_mse,
x0=[0.5, -0.5],
args=(home, draw, away),
options=options,
)
output = {
"home_exp": np.exp(res["x"][0]),
"away_exp": np.exp(res["x"][1]),
"error": res["fun"],
"success": res["success"],
}
return output
Our goal_expectation function takes the bookmaker's odds as inputs and returns the number of home and away goals predicted by the bookmaker.
The first part of the function just sets up some options to tell the minimizer to give up if it's not found a decent answer after 1000 attempts and not to print out a whole load of messages to the screen while it's doing it.
Next, we run the minimizer by passing in the function to minimise the error for. We also pass in some starting parameters for the home and away goals as x0 to give the minimizer a head start. Finally, we pass in the bookmaker's probabilities and the options we set up. We wrap things up by formatting the output from the minimizer to just return the information we're interested in.
Let's give it a go!
output = list()
for _, row in df.head().iterrows():
res = goal_expectation(row["psh"], row["psd"], row["psa"])
tmp = {
"team_home": row["team_home"],
"team_away": row["team_away"],
"home_exp": res["home_exp"],
"away_exp": res["away_exp"],
"success": res["success"],
"error": res["error"]
}
output.append(tmp)
output = pd.DataFrame(output)
print(output)
| team_home | team_away | home_exp | away_exp | success | error | |
|---|---|---|---|---|---|---|
| 0 | Crystal Palace | Arsenal | 0.837309 | 1.470508 | True | 8.111775e-12 |
| 1 | Bournemouth | Aston Villa | 0.921695 | 1.406204 | True | 6.030584e-10 |
| 2 | Everton | Chelsea | 0.727779 | 1.693048 | True | 6.227654e-12 |
| 3 | Fulham | Liverpool | 0.680463 | 2.510449 | True | 2.981267e-11 |
| 4 | Leeds | Wolves | 1.187333 | 0.960074 | True | 2.442655e-09 |
The success column shows lots of True values, meaning the minimizer successfully found a solution each time and the error column is full of lots of tiny numbers meaning our predictions should be pretty accurate 😃
Conclusions
This technique should give you decent estimates but there's still some room for improvement. If you go back to my article on the Dixon and Coles model, I discussed how the Poisson distribution can struggle somewhat with the probabilities for low scoring games and how Dixon and Coles used an adjustment factor to try and alleviate this.
We can also include this adjustment into our loss function to try and reduce our error even further. I haven't added it in here as I wanted to keep this article simple but you can try the Dixon and Coles adjusted version in my penaltyblog package by using the pb.models.goal_expectancy function.
Addendum
Just to make clear for anybody who is unsure, the goal expectancy discussed here is different to expected goals. Goal expectancy is how many goals the bookmaker is expecting based on their 1x2 odds, whereas expected goals is how many goals a team is expected to score based on the shots they have taken. They both have similar names but quite different meanings.